Understanding Perimeter
We all know that there are many classifications of Polygons, and one of those is QUADRILATERALS, a 4 sided polygon. There are many examples of quadrilaterals, but most common quadrilaterals are SQUARE, RECTANGLE and PARALLELOGRAM. In this topic, we will be discussing on how to calculate the perimeter of a square, rectangle and parallelogram.
Perimeter is the distance around a two-dimensional shape. Two-dimensional shape, are shapes with two dimensions such as width and height, and perfect example of two dimensional shapes are square, rectangle and parallelogram.
Below is a short description on understanding perimeter of Square, Rectangle and Parallelogram
Let’s first understand the perimeter of a square. As we all know, a square is a quadrilateral with 4 equal sides. Meaning, side a = side b = side c = side d. For better understanding, see illustration below
How to Calculate the Perimeter of a Square
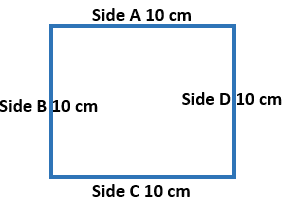
So to compute for the perimeter of a square, we do follow this simple formula:
P = a + b + c + d
Where: P = Perimeter
- A = Side A
- B = Side B
- C = Side C
- D = Side D
Or P = 4.S
Where: P = Perimeter S = Sides
Since a square has a uniform dimensions of the sides.
Let’s take this as an example:
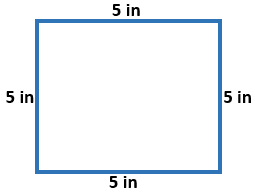
Shown is a square with a side dimension of 5 inches. Find the perimeter.
Solution:
P = a +b +c + d OR P = 4.S
P = 5 + 5 + 5 +5 P = 4 x 5
P = 20 inches P = 20 inches
Any solution or formula you used will still result to the same answer.
How to Calculate the Perimeter of a Rectangle
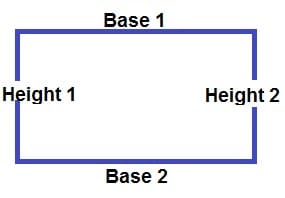
And now, I will let you know how to compute for the perimeter of a rectangle. Though square and rectangle are both quadrilaterals, but still a RECTANGLE has different sides, wherein Base 1 = Base 2, while Height 1 = Height 2.
See illustration below:
So to compute for the perimeter of a rectangle, we will be using this formula:
P = 2.B + 2.H
Where:
- P = Perimeter
- B = Base 1 and 2
- H = Height 1 and 2
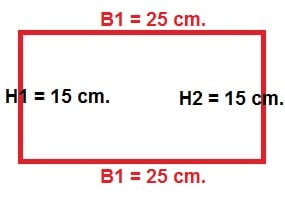
Using the formula, we can identify that B = 25 cm. and H = 15 cm. So now were ready to solve
P = 2.B + 2.H
P = 2 x 25 cm + 2 x 15 cm
P = 50 cm + 30 cm
P = 80 cm.
So the perimeter is equal to 80 cm.
Hint:
In some Math questions, the perimeter and either the base or height is given. In this case, we could still use the same formula, but just equate this to the needed requirement
P = 2.B + 2.H
P = 2 x 25 cm + 2 x 15 cm
P = 50 cm + 30 cm
P = 80 cm.
So the perimeter is equal to 80 cm.
Hint:
In some Math questions, the perimeter and either the base or height is given. In this case, we could still use the same formula, but just equate this to the needed requirement
How to Calculate the Perimeter of a Parallelogram
So now, we will move on to computing the Perimeter of a Parallelogram. Just like a rectangle, a parallelogram is a quadrilateral with two different sides; the only difference is that a parallelogram has two parallel sides, to further understand see illustration below:
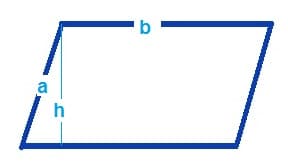
As shown in the illustration, there are three essential parts of a parallelogram:
- Side a, which is parallel to the opposite side
- Side b, which is parallel to the opposite side
- And h, which is the horizontal height
Since the sides of a parallelogram are parallel to each other, the formula to be used in computing for its perimeter is:
P = 2 (a +b) where:
- P= Perimeter,
- a = side a, and
- b = side b.
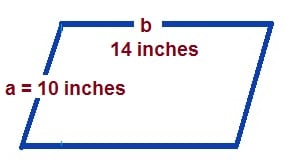
Lets try one example
Since b = 14 inches, a = 10 inches. We can now compute for the perimeter
Solution:
P = 2 (a +b)
P = 2 (10 + 14)
P = 2 (24)
P = 48 inches
Test your knowledge on Perimeters
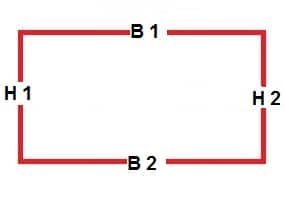
Based on the below rectangle answer the next 3 questions
Are you ready to practice more tests on Perimeter why not sign up
